kdh22q

1. GIS 설치 : postgres 설치시 stack builder 에서 gis를 같이 설치 또는 이미 postgres가 설치되어있으면 stack bulider 파일을 찾아 실행하여 Spatial Extensions > gis를 설치

2. GIS 활성화 : 

CREATE EXTENSION postgis;

3. 토폴로지 활성화 : 

CREATE EXTENSION postgis_topology;

1. 기초통계량 :

데이터를 요약해서 이해하기 쉽게 보여주는 숫자.

   1) 평균(average) : 모든 데이터를 더하고 데이터 개수로 나눈 수, 데이터 전체를 한눈에 보여주는 대표값, 엄청 크거나 작은수가 있으면 평균이 왜곡될 수 있음.

   2) 중앙값(median) : 데이터를 크기순으로 정렬했을 때 가운데 있는 수, 데이터 개수가 짝수면 가운데 두 수의 평균을 구함, 극단적인 수의 영향을 덜 받음.

   3) 최빈값(mode) : 숫자들 중 제일 자주 나온 수, 모든 수가 동일하게 나오면 최빈값 없음,

   4) 범위(range) : 숫자들 중 제일 큰 값에서 제일 작은 값을 뺀 수.

   # 중심 경향도 : 데이터의 대표값을 찾아서 복잡한 수자 더미를 간단하게 이해하도록 해줌.

2. 평균의 종류

   1) 산술평균(arithmetic mean) : 숫자들을 다 더해서 숫자의 개수로 나누는 방법, 전체적인 크기를 고르게 반영할 때 좋음.

   2) 기하평균(geometric mean) : 숫자들을 곱한 뒤 그 곱의 n번쨰 루트를 구하는 방법, 곱셈 관련 상황에서 사용(주식수익률, 인구 증가율 등)

   3) 조화평균(harmonic mean) : 숫자들의 역수를 더하고, 그 합을 숫자 개수로 나누고, 다시 역수로 바꾸는 방법, 속도, 효율, 비율처럼 단위당 계산이 중요한 경우 유용.

   4) 절사평균(trimmed mean) : 데이터 양 끝의 극단적인 값을 제거하고 남은 수의 산술평균을 구하는 방법. 이상치의 평균 왜곡을 막는 방법.

3. 산포도 :

중심에서 얼마나 떨어져 있는지를 측정. 데이터가 평균 근처에 몰려있으면 산포도가 작고, 멀리 퍼져있으면 산포도가 큼.

4. 변동계수 :

데이터의 퍼짐정도(산포도)를 데이터의 평균으로 나눠서 백분율로 나타낸 것. 평균에 비해 얼마나 흩어져 있는지 퍼센트로 보여줌. 데이터의 단위가 달라도 퍼짐정도를 공정하게 비교하도록 해줌.

 

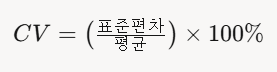
5. 사분위수 : 

4개의 같은크기 그룹으로 나누는 값들. 데이터를 작은것부터 큰 것까지 정령하고, 20%, 50%, 75%, 100%지점에서 나눔. 데이터의 퍼짐정도를 보여주고, 이상치에 덜 민감하여 데이터의 가운데 부분을 분석할 때 유용. 데이터의 분포를 이해하거나 이상치를 찾을 때 유용.

6. 비대칭도 : 

   1) 왜도 : 데이터 분포의 모양이 치우친 정도의 수. 분포의 모양을 이해할 수 있음.

      (1) 왜도 = 0(대칭분포) : 데이터가 평균을 중심으로 대칭

      (2) 왜도 > 0(오른쪽으로 치우친 분포, 양의 왜도) : 데이터가 오른쪽으로 긴 꼬리를 가짐

      (3) 왜도 < 0(왼쪽으로 치우친 분포, 음의 왜도) : 데이터가 왼쪽으로 긴 꼬리를 가짐

      (4) 수식 : 각 데이터가 평균에서 얼마나 떨어져 있는지를 세제곱한 뒤, 평균을 내고 표준편차로 나눠서 구함.

   2) 첨도 : 데이터의 분포 모양이 얼마나 극단적인지, 가운데가 뾰족하거나 납작한지를 측정.

      (1) 중첨도 : 데이터 분포가 정규분포와 비슷함.

      (2) 고첨도(첨도 > 0) : 분포가 정규분포보다 더 뾰족하고 꼬리가 두꺼움. 데이터가 평균 근처에 많이 몰려있는 경우.

      (3) 저첨도(첨도 < 0) : 분포가 정규분포보다 더 납작하고 꼬리가 얇음. 평균근처에 덜 몰리고, 극단적인 값이 적음.

      (4) 수식 : 데이터가 평균에서 얼마나 떨어져 있는지를 네제곱한 뒤, 평균을 내고 표준편차로 나누서 구함.

1. 기술통계 : 표본을 통해 얻은 정보를 설명하는 방법, 모집단을 대표하고 있다는 것을 주장하기 위함.

2. 도수분포표 : 수집된 각각의 데이터에 대한 개수를 정리한 표

3. 히스토그램 : 도수분포표의 측정치들을 계급으로 구분하여 측정치의 개수를 표현

4. 상자수염그림 : 2개 이상의 집단 자료를 서로 비교할 때 사용, 최대값, 최소값, 평균, 중앙값, 등의 정보 제공(표현에 유리)

1. 변수 : 대응관계로 변하는 수

2. 데이터 : 조사의 목적에 맞는 변수를 통해, 표본에서 수집된 자료

3. 척도 : 설문지를 통해 데이터를 수집할 때 활용되는 기준

   1) 범주형 척도 : 데이터들을 구분지어 나눌 수 있는 척도

      (1) 명목척도 : 순서의 개념과 상관없이 이름만 붙인 척도 (예시 1.남자 2.여자)

      (2) 서열척도 : 연산과 연관없이 순서를 구분할 수 있는 척도(예시 1등 2등 3등)

   2) 연속형 척도 : 연결된 속성의 데이터를 조사의 목적에 맞게 구분한 척도

      (1) 등간척도 : 간격이 일정한 수치 데이터, '0' 의 간격차이를 비교할 수 있음(예시 섭씨 10도, 섭씨 0도 에서 0도는 없음을 나타내지는 않음)

      (2) 비율척도 : 간격이 일정하면서도 절대적인 0(없음) 이 존재하는 수치 데이터, 비율 비교가 가능(에시 0kg - 무게 없음, 10kg는 5kg의 두배)

1. 표본분포 : 모수를 추정하기 위한 표본 분포

2. 표본평균의 오차 : 전체 평균과 표본평균 사이에 생기는 차이, 표본개수가 늘어날수록 통계량이 모수와 가까워짐

3. 중심극한정리 : 표본의 평균 분포가 정규분포에 가까워짐, 원래의 데이터가 정규분포가 아니어도 가능, 이를 통해 정규분포 기반 통계기법을 광범위하게 적용 가능

• μ: 모집단 평균
• σ2\sigma^2σ2: 모집단 분산
• nnn: 표본의 크기
• Xˉ\bar{X}Xˉ: 표본평균
• N(...)N(...)N(...): 정규분포

내가 이해해보기 위한 중심극한정리  예시:

- 모집단 = [2, 4, 6, 8]
- (총 4개의 숫자, 이게 전체 데이터 = 모집단)

- 이제 크기 2짜리 표본을 가능한 모든 조합으로 뽑는다.

여기에서 표본평균의 평균은 :

(3+4+5+5+6+7) / 6 = 5.0

모집단의 평균은 :

(2+4+6+8) / 4 = 5.0

이므로 표본평균의 평균은 점점 모평균에 수렴하게 된다.

1. 표준화

   1) 정규분포 : 표본분포 중 가장 단순하고, 많이 발생하는 분포, 사건의 빈도에 따라 평균을 기준으로 좌우 대칭

   2) 표준화 : 여러 특성에 대한 기준점을 동일하게 맞춰 조사자가 자료를 쉽게 비교 가능하도록 만드는 것, 표준정규분포는 평균 0, 표준편차 1

• X : 원래의 값
• μ : 평균 (mean)
• σ : 표준편차 (standard deviation)
• Z : 표준화된 값 (Z-score)

   3) z분포(표준정규분포) : 표본의 개수가 충분할 때 표준화를 거친 정규분포, 평균 0, 분산 1

   # Z분포표

   4) t분포 : 모집단의 분산을 모르고 표본의 개수가 충분하지 않을 때(30개 이하) 사용하는 정규분포, 평균 0, 분산 > 1

• s: 표본 표준편차
• n: 표본 개수
• μ: 비교 대상인 모평균
• t-score는 Z-score와 비슷하지만, 표준편차 대신 표본 표준편차를 사용

   5) χ²분포 : 분산의 분석, 적합도 검정, 독립성 검정에 사용하는 분포, 표준 정규분포(Z)의 제곱들의 합, 적을수록 비대칭, 클수록 정규분포에 가까워짐

​

• O: 관측값
• E: 기대값

   6) F분포 : 두 정규분포에서 추출한 표본들의 분산 비율 분포, 두 카이제곱 분포를 자유도로 나눈 비율

​

​

• S1^2,S2^2 ​: 각각 두 표본의 분산
• ν1,ν2​: 각각 두 표본의 자유도

   7) p^(p hat)분포 : 표본비율의 분포, 모비율을 추정할 때 사용

      (1) 모비율 p : 모집단 전체의 어떤 특성을 가진 비율

      (2) 표본 비율 p^ : 표본에서 조사한 비율

• p : 모집단 모비율
• n : 표본 크기
• p^ : 표본 비율

# 수식의 의미를 이해해보자!

• 표본비율을 가지고 모비율을 추측하는 것이 목적이다. 따라서 표본이 얼마나 평균에서 벗어나 있는지를 측정하고 비교해야한다. 
• p^ - p는 관측한 값과 원래값의 차이를 확인
• 나누기를 통하여 비교 기준을 설정(표본 비율의 표준편차, 흔들림 정도)
• 분모의 표준편차 수식 : 이항분포의 분산은 p(1-p)이다. 그리고 n번 뽑은 표본평균을 사용하기 때문에 n으로 나누어준다.

따라서, 전체 수식의 의미는 z = 실제차이 / 흔들림 정도 이고, 차이가 크면 귀무가설 기각, 차이가 적으면 귀무 가설을 유지하는 방향으로 설정하게 된다.